WORK WITH SPREADSHEETS
Directions: |
My Work: |
THE LOCKER PROBLEM
The Problem:At a large high school, there are 1000 lockers all on one wall of a long corridor. The lockers are numbered, in 1, 2, 3 ... 1000, and to start, each locker is closed. There are also 1000 students, also numbered 1, 2, 3 ... 1000. The students walk the length of the corridor, opening and closing lockers according to the following rules:
1) Student #1 opens every locker. 2) Student #2 closes every second locker. 3) Student #3 changes the state of every third locker, closing it if it is open, and opening it if it is closed ... k. 4) Student #k changes the state of every k-th locker. a) When all 1000 students have walked the corridor, which lockers end up open? b) Which locker is touched the most? My Work Explained:I started out by knowing that the locker that will be touched the most will not be prime and will be even. I then replicated this scenario using a drawing with 10 lockers and 10 people. I then transferred this to my spreadsheet. I found that the numbered locker(s) with the most factors will be touched the most. My spreadsheet also showed me that the ones that are left open are all perfect-squares.
|
Final Work:We came to these conclusions, as a team:
The lockers left open are perfect squares: 1, 4, 9, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 900, and 961. The locker(s) touched the most is the one with the most factors: 840. We created an extension question: Which people should we not let through, in order to only have locker #1 open. We tried this with 20 lockers and people, and found that in order to achieve our goal, we couldn't let 4, 8, 9, 12, 16, 18, and 20 through. |
NUMBERS AND OPERATIONSThe Problem:1) Consider all six digit numbers formed by using the digits 1,2,3,4,5, and 6 exactly once. What is the sum of all of these six digit numbers?
2) Take a three digit number, reverse its digits, subtract the smaller from the larger. Now, reverse the digits of this difference and add it to the original difference. Try this process with several numbers. What do you observe? Can you explain why this happens? 3) Find all positive integers "a" where a^10+1 is divisible by 10. My Work Explained:1) I found that the total number of six digit numbers is 720. I found this by doing six-factorial (6!) or 6*5*4*3*2*1=720. After knowing that, I also found that for every in that bunch, there is an opposite number that adds to 777,777. Therefor, there are 360 pairs of numbers that add to 777,777. If you do 360*777,777=279,999,720. So the sum of all of these six digits numbers is 279,999,720.
2) I tried this with multiple number sequences and found that all of the operations ended with 1089 or 198. I could not explain why this happens. 3) After guessing and checking, I found that the positive integers of "a" that could give an answer divisible by 10 were all number ended 3 or 7. |
Final Work:1) I was correct. The answer was 279,999,720.
2) This can be explained by the equation 99(a-c). 3) I was correct. The variable "a" must end in 3 or 7 to produce an answer divisible by 10. |
PROBLEMS WITH PROBABILITY
The Problem:1) James and Claire just had a nasty break-up and are hoping they don't have to see each other. However, they still each get coffee at the same place each morning. On any given day, they will arrive separately at a random time between 7:00 and 7:30. They'll each be in the shop for a total of 5 minutes. What is the probability that they'll both be int he coffee shop at the same time?
2) If 2 points are placed on the perimeter of a square with side length L, what is the probability that the distance between them is <1? 3) If 3 points are placed randomly on the perimeter of a circle, what is the probability they will form an acute triangle? What if they could also be placed on the interior of the circle? What is the probability that the center of the circle is inside the triangle? 4) Can you come up with your own problem that would be modeled in the same fashion? My Work Explained:1) I originally recognized that it could easily be ∞/∞. Although, if we look at it by minutes, the probability is different every minute from 7:00 to 7:30. I found the probability for every minute, and represented it in a table (see Table 1). I graphed this table (see Graph 1) and found the average probability to be 9.03/31. After discussing with Dan, I found another graph (see Graph 2). The middle line represents the time that each person came in and the shaded region represents the time they may run into each other. I plan to put the area of the shaded region as the numerator and the denominator will be 900.
3) I started out by recognizing that a circle is 360 degrees. If the second and third points hit the 90 degree mark from the first point, then the triangle will be right. But if the points are after the 90 degree mark, then it will be acute. The probability I found was 89/180 for acute, 89/180 for obtuse, and 1/90 for right. After discussing with Dan, I found that after two points are placed randomly, the third point must be placed between points parallel to the first and second points. This is proved correct. Probability for this has not yet been found. |
Final Work:1) We continued with the work and used my graph to find the probability to be 275/900, which can be simplified to 11/36. 900 is the total area of Graph 2. 625 is the total area where they will not run into each other on Graph 2. Which leaves 275 as the area representing where they may run into each other.
2) We began to work on this problem as a team, and peers showed what they had found, but we ran out of time with the special schedule. |
THE GAME OF 24
The Problem:Using each of the numbers below exactly once and any of the 4 basic operations, make the number 24:
4,6,6,1 2,9,3,8 3,9,4,4 2,7,9,3 8,3,4,7 Using the numbers 1,2,3, and 4 no more than once, and any of the operations of addition, subtraction, and multiplication, what is the largest number you can obtain under these restrictions? Extension Questions: - What is the smallest positive number you cannot get? - What is the smallest negative number you can get? - What if we allow another operation such as division? My Work Explained:I decided to start with the second part of the problem and the extension questions as they interested me more. I found that the largest number I could obtain under the restrictions given was 36. I found that the smallest positive number that I couldn't get was 27. I found the smallest negative number I could get was -23. I also produced work with the operation of division. I never got around to answering the actual problem.
|
Final Work:As a team, we found that 29 was the smallest positive number we could not get. We found that we could 27 by ((4*2)+1)*3. No prime number over 27 can be reached. We discussed how the problem would change if we were able to use operations such as exponents, limits, and asymptotes.
|
TWO COLORED TRIANGLE GAME
The Problem:Place six dots in a hexagonal array. Number them. To play the game, players take turns connecting any two unconnected dots with either of two colors. Players may switch colors any time they choose. Once a line is drawn, it may not be re-drawn or have it's color changed. The game ends when a player completes a triangle on three of the numbered dots that has all sides in the same color - that player then loses.
My Work Explained:After playing the game with a partner many times, we found the equation for the number of lines that can be drawn based on the number of vertices to be L = ^(x-1)∑n where n = 1. It can also be represented by the equation L = .5x²-.5x . I found that there can not be a tie given six vertices. I dabbled in the possibility of adding a third color or changing the number of vertices.
|
Final Work:Working with the whole team, we came to these conclusions:
- There must be 3 lines of the same color coming off one vertex. - The 15th line will be drawn by the player that goes first. - Possible strategies include: Mirror the 2nd player, attempt to draw "kill boxes", attempt to draw safety lines. - When a "kill box" is made, two triangles will be made. |
BOOMERANG FRACTIONS
The Problem:Choose a fraction m/n. Begin a sequence of number with 1. To get the next number of the sequence, add m/n. On subsequent steps, either add m/n or take the reciprocal. We say that the longevity of the fraction is the minimum number of steps needed to return to 1.
My Work Explained:NOTE: In the equation of m/n, m = 1.
After independently working and working with others, I found these formulas -- If "n" is odd: L = n² If "n" is even: L = 1.5n+1 Final Work:Working with the whole team, we came to these formulas --
If "n" is odd: L = 2n+(n²-n/2) If "n" is even: L = 1.5n+1 |
|
TOPOGRAPHICAL MAPS
|
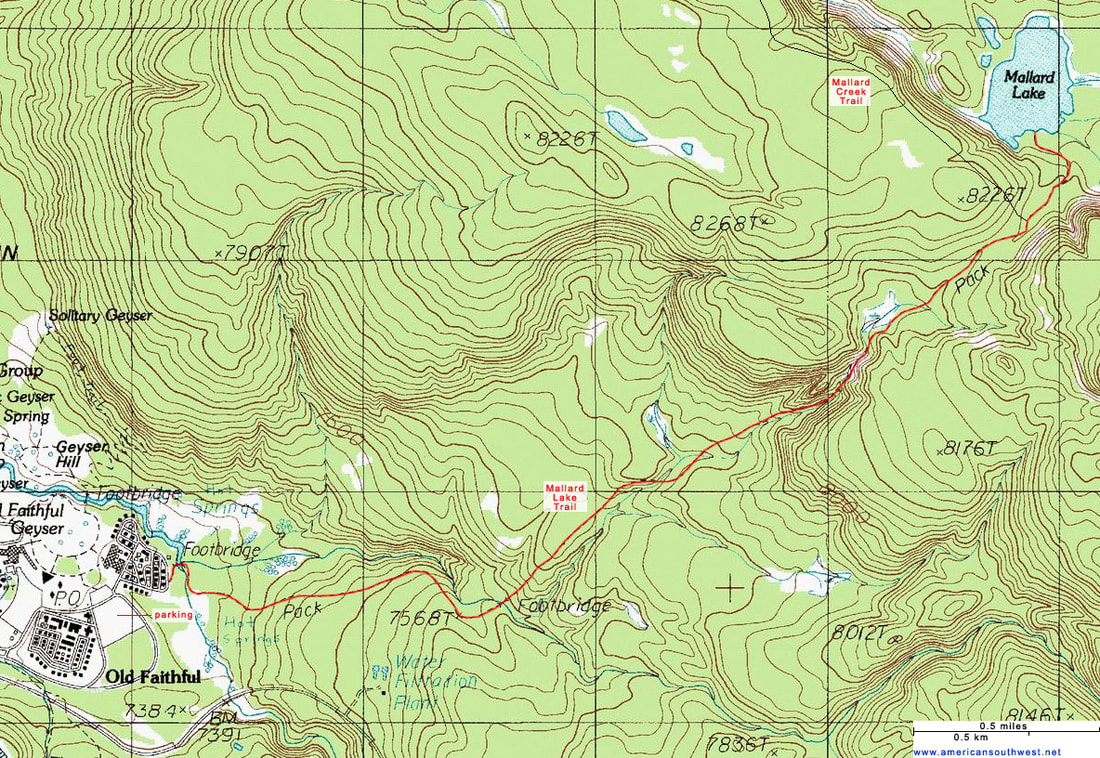
http://www.americansouthwest.net/wyoming/yellowstone/mallard-lake-map.html
|
We started out this unit by attempting to draw a 3D object using angles. We called these isometric drawings. We then went on to learn about Pentominoes and take an educated guess as to how many pentominoes can be created into an open box. "A pentomino (or 5-omino) is a polyomino of order 5, that is, a polygon in the plane made of 5 equal-sized squares connected edge-to-edge." After that, each person at our table group found a coordinate for a certain location in Durango. We put all four coordinates onto a map, determined our range, and determined a suitable scale. We then had to measure the distance (in meters) between all points using our scale. This is when we started learning about topographical maps using in class labs. For instance, Dan created miniature mountain ranges in cardboard boxes and we had to attempt to draw the "bird's eye view" on paper. We learned about the different shapes that the lines make in topographical maps and how use those shapes to tell what type of "structure" is there (i.e. canyon, peak, ridge, etc). We used all this knowledge to find locations in the forest in groups on our sophomore camping trip. There were a total of 12. My group found 3 in 2 hours by using a coordinate GPS, a list of the coordinates, and a map. We reflected on this unit by asking the question, "What needs to happen in group work for the group to be successful?"
|
Header Image Site: Provided by Weebly